임시
토글
//책에서 9번!
Raytracing One Weekend 식 이해하기! 7
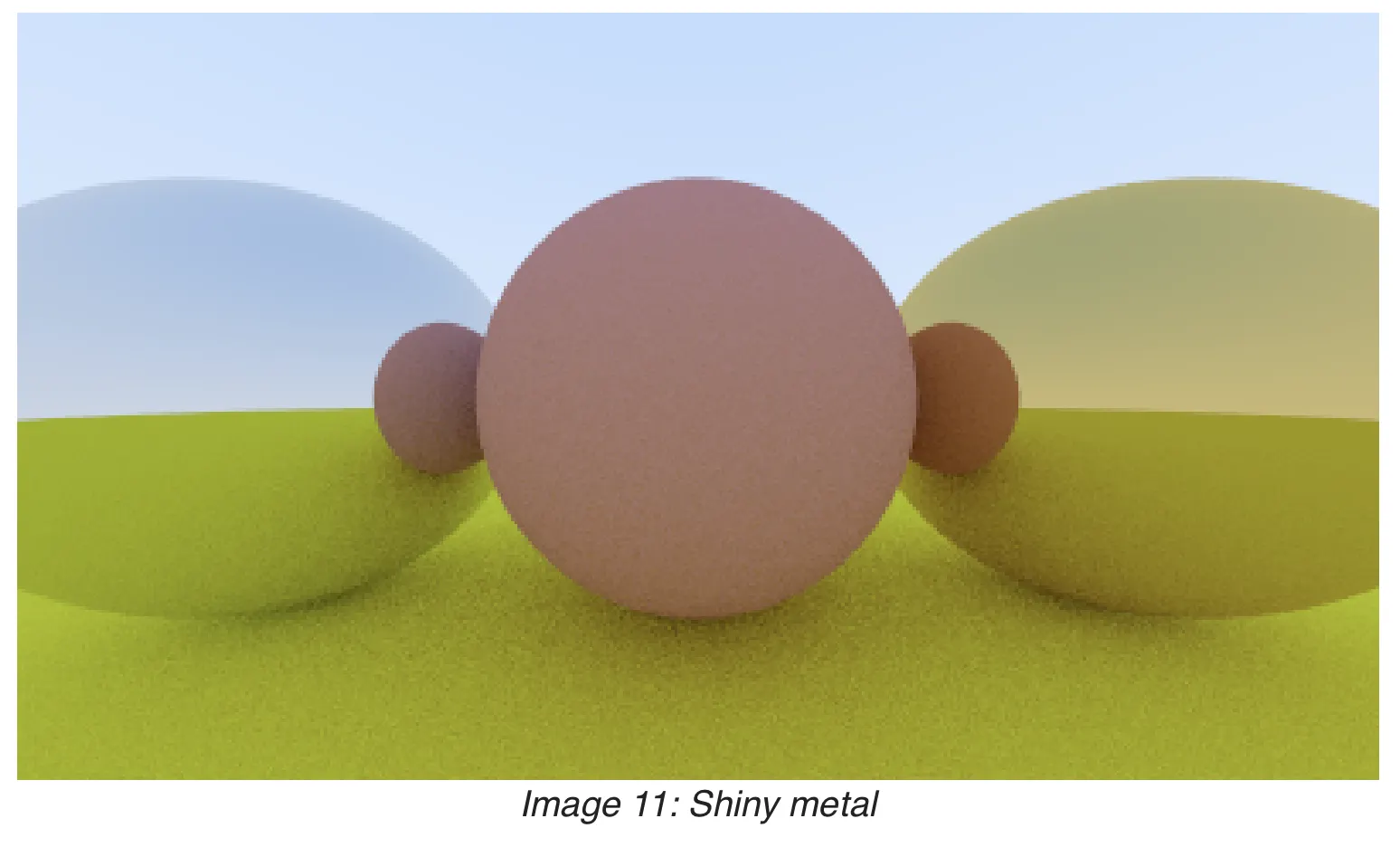
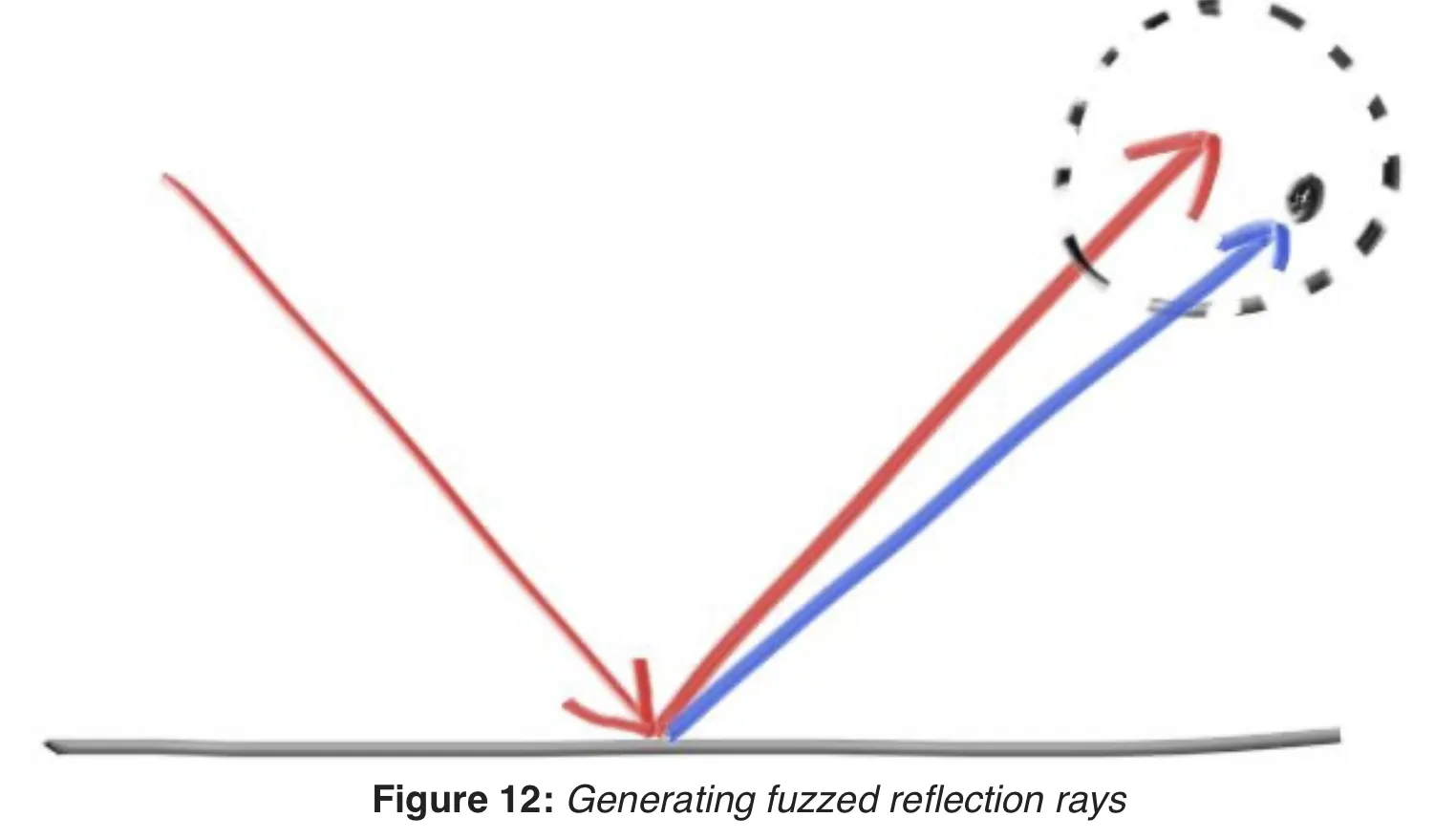
철과 같이 표면이 맨들맨들한 물체들은 주변 물체가 반사돼서 보이곤 한다. 이번 파트부터 도형의 다양한 표면을 구현해 볼 것이다.
Metal
1) An Abstract Class for Materials
우선 Metal표면을 구현하기 전에 본문에서는 다양한 표면을 대비해서 미리 추상클래스를 만들어둔다. 해당 추상클래스 내부에는 물체와 부딪히고 흩어진 ray에 대한 함수가 작성되어 있다. 우선 C언어로는 추상클래스를 만들순 없으니 이후 일반 함수로 만들어서 사용할 예정이다.
개인 코딩스타일에 맞게 함수포인터 등을 활용해서 구현하는 것도 좋아보인다.
이번 장 이후 부터는 이떄까지의 코드가 모두 다르기때문에 예시로 나온 코드를 본인의 코드에 적용시키기는 어려워 보인다. 조금씩 수정하면서 어떤 변수들이 필요하고 결과적으로 필요한 값이 뭔지 이해한다면 코드를 작성하는 것도 크게 어렵지 않다.
2) A Data Structure to Describe Ray-Object Intersections
이제 모든 오브젝트들이 material을 가지고 있을 것이기 때문에 hitt 구조체와 hit함수에 해당 부분을 추가해 주어야 한다. 그리고 이후 hit 함수에서도 부딪힌 지점의 matarial을 가지고 와야하기 때문에 hit_record에도 해당 지점을 저장해 두어야 한다.
// hit_record 구조체에 저장
typedef struct s_hit_record
{
...
t_material *material; // 물체의 재질을 저장하는 구조체
}
C++
복사
수정된 부분은 아직 추상함수들 밖에 없기 때문에 아직 이해가 안되는 부분이 있다면 아래부분부터 먼저 공부한 후 다시 앞부분을 보는 것도 좋다. 내부에 들어가야할 함수들에 대한 설명이 지금부터 나온다.
3) Modeling Light Scatter and Reflectance
이전파트에 나왔던 lambertian 부분에서 우리가 생성한 랜덤 분산 벡터와 법선 벡터가 정확히 반대방향인경우, 우 벡터의 합이 0이 되어서 분산방향벡터가 0이 된다. 이렇게 되면 이후 계산에서 0 또는 무한대가 발생하므로 사전에 차단할 필요가 있다. 아래 식에서는 0과 근사치에 가까워지는 경우 랜덤 분산벡터를 법선백터로 바꾸어주는 식이다.
near_zero() 함수를 활용해서 벡터가 0과 가까워지는 것을 판단한다.
// C++ code
bool near_zero() const {
// Return true if the vector is close to zero in all dimensions.
const auto s = 1e-8;
return (fabs(e[0]) < s) && (fabs(e[1]) < s) && (fabs(e[2]) < s);
}
// C code
int near_zero(t_vec v)
{
int limit;
limit = 10000000;
return ((v.x < limit) && (v.y < limit) && (v.z < limit));
}
C++
복사
이후 조건문 하나를 추가해주기만 하면 끝이다.
if (scatter_direction.near_zero())
scatter_direction = rec.normal;
C++
복사
4) Mirrored Light Reflection
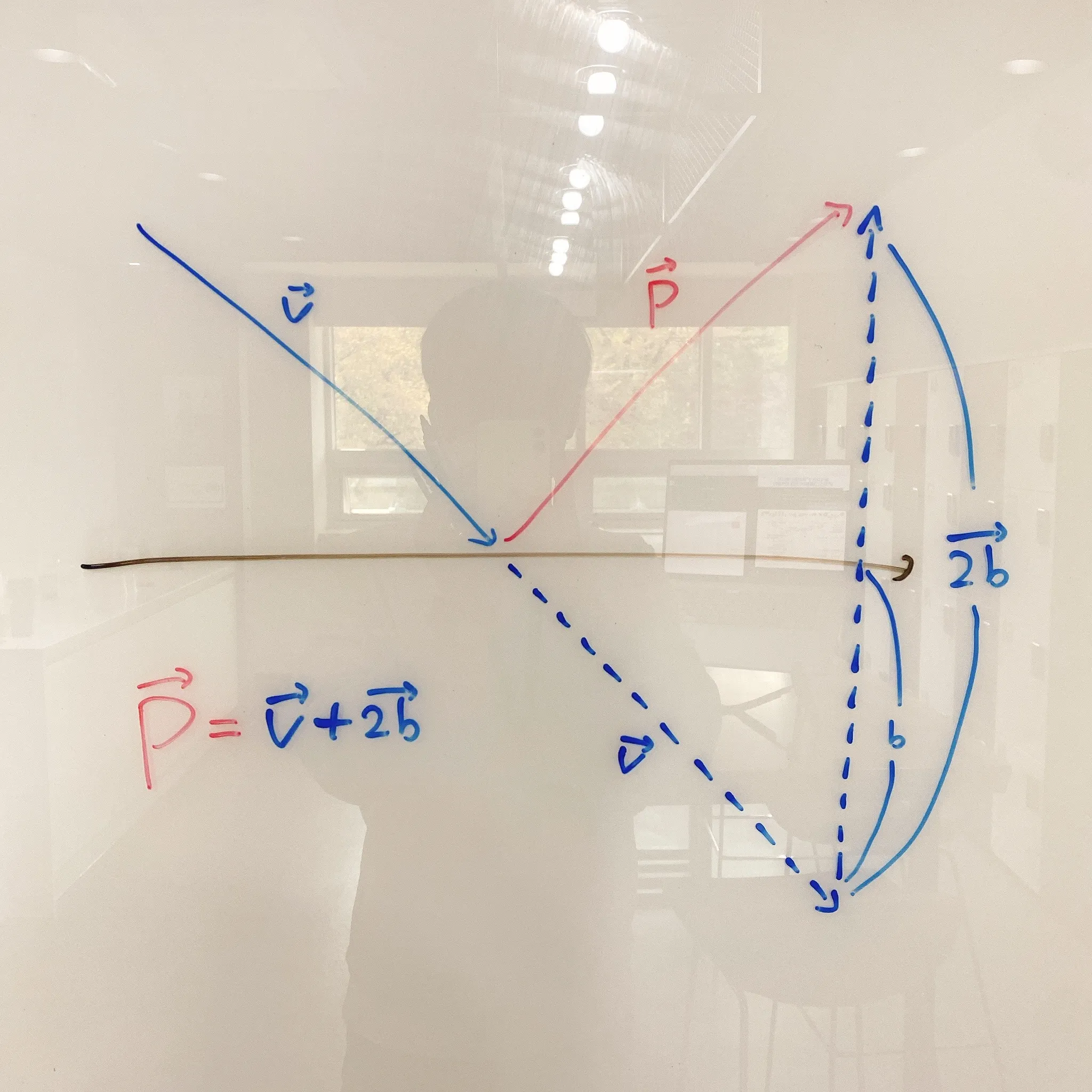
이제 드디어 거울반사되는 벡터를 만들어볼 예정이다. 아래 사진을 보자!
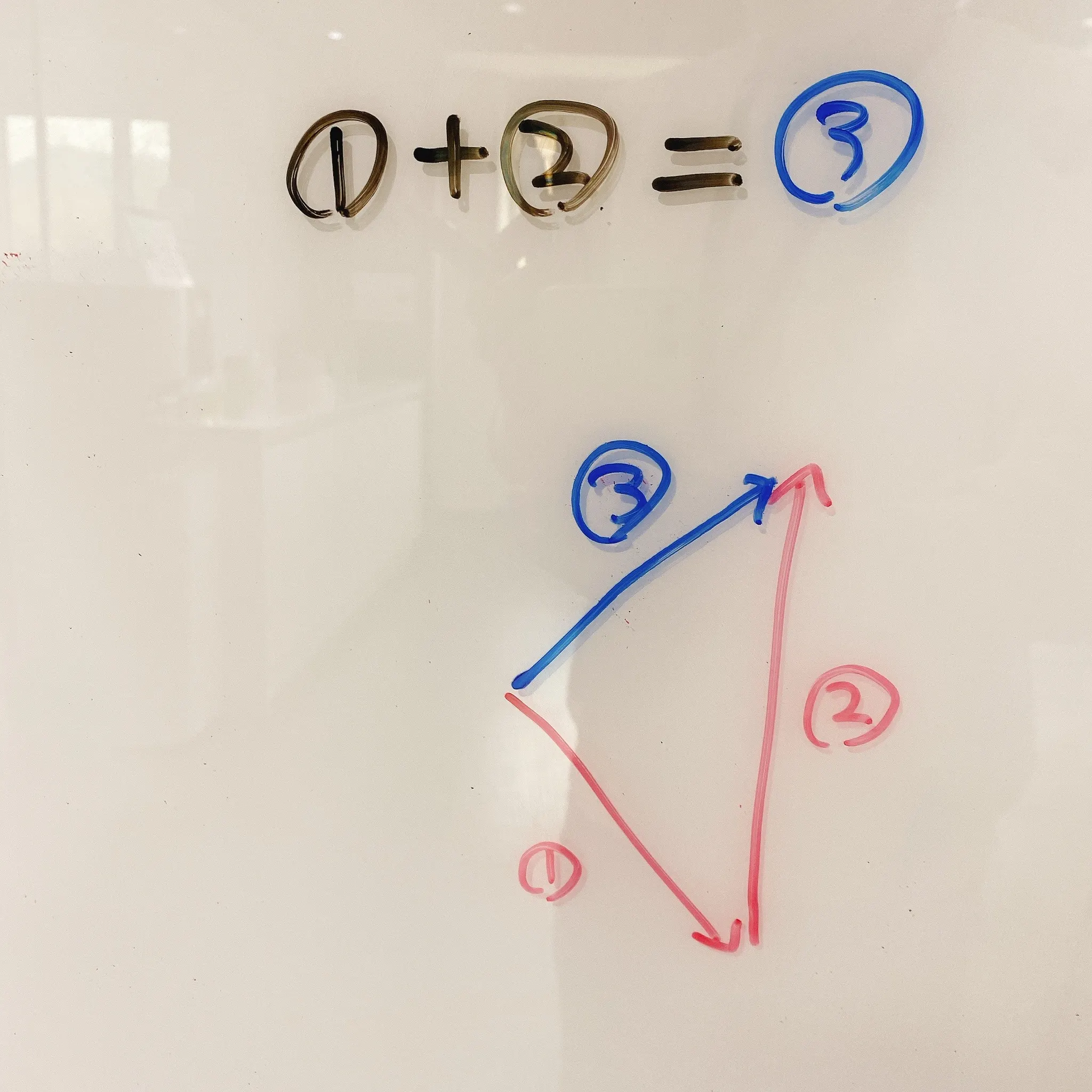
우리는 들어오는 V벡터를 가지고 P벡터를 만들어야한다. 교재에서는 아래와 같은 유도방법을 사용하고 있다! 즉,
이때 우리는 V를 이미 알고있으므로 b벡터만 구하면 된다. 이때 우리는 내적을 사용할 수 있다. 아래와 같이 식을 유도할 수 있다!