//책에서 8번!
Raytracing One Weekend 식 이해하기! 6
이번 시간에는 Diffuse에 대해 알아보자!!
번역을 해보면 확산(?) 이라고 나온다! 즉, 이번 장에서는 종이나 테이블과 같이 어떤 방향에서 보던 해당 물체가 같게 느껴지는 모양을 만들어 볼 것이다. 이부분을 끝내면 아래와 같은 결과물을 만들 수 있다!!
diffuse reflection?
빛이 여러 각도로 반사되어 선명한 이미지가 없을 때 생기는 효과(난반사)
Diffuse Materials
1) Matte surfaces
이제 본격적으로 매트 재질을 표현해보자! 빛이 구의 표면에 부딪히면 무작위로 확산하게 된다! 표면이 거칠거칠한 탱탱볼 같은 것을 생각해보자! 표면에서 반사되는 빛의 방향은 우리가 예상하지 못하는 방향으로, 즉 무작위로 퍼지게 된다.
오른쪽 그림의 위는 Specular Reflection, 아래가 Diffuse Reflection이다.
여기서 추가적으로 이러한 재질의 표면은 빛을 완전히 반사하는 것이 아니라 일정부분 흡수하게 된다. 즉 반사가 계속 이루어질수록 흡수되는 빛의 양이 많아져서 점점 빛이 어두워지게 된다.
반사된 ray가 어떤 색을 가져올까?
챕터를 시작하기 전에 하나의 구조를 먼저 이해하고 넘어가자!
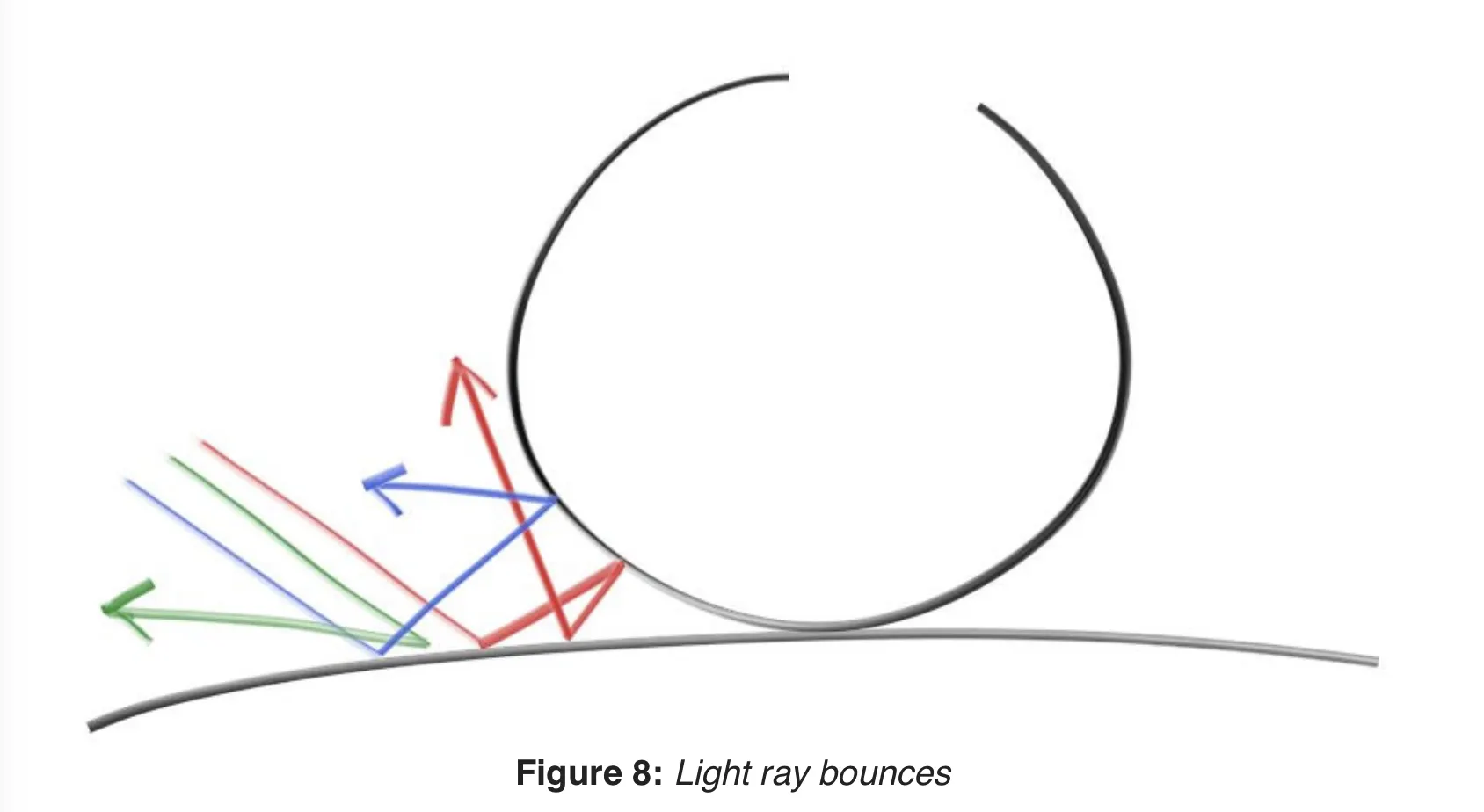
반사된 ray가 다음 물체에 부딪혔을때 그 색을 어떻게 가져오는 것일까? 책에서는 재귀함수를 활용해서 이것을 해결했다. 아래 그림을 보자!
각 ray를 색깔별로 표기했다. 각 주황 핑크 빨강 보라 ray가 위 사진들과 매칭된다.
처음 쏜 ray가 구 C1에 부딪힌다. 이때 diffuse reflection된 빛이 구 C2 쪽으로 향했다고 생각해보자. 그리고 이 ray가 다시 C2에 부딪힌 후 다시 반사되어 C1으로 향하고 마지으로 C1에 부딪힌후 반사된 ray는 부딪힐 물체가 없는 곳으로 끝없이 향하게 된다.
이때, 각 ray는 반사된 ray가 가져오는 색을 리턴한다! 즉, 아래 의사 코드처럼 재귀적으로 동작하는 것이다.
t_color ray_color(특정 지점에서 쏘는 ray, 오브젝트들을 가지고 있는 구조체 world)
{
만약 ray가 물체와 부딪혔다면
{
new_ray = 난반사 ray를 만든다.
return ray_color(new_ray, 오브젝트들을 가지고 있는 구조체 world); // 재귀함수!
}
y벡터를 기준으로 그라데이션을 만든다(하늘 색상)
return 하늘색
}
C++
복사
이때 무한히 물체들과 부딪히는 경우가 생길 수 있고 기대한 횟수보다 많이 반사될 수 있기 때문에 탈출 조건을 추가해준다.
t_color ray_color(특정 지점에서 쏘는 ray, 오브젝트들을 가지고 있는 구조체 world, 최대반사횟수)
{
만약 최대 반사횟수를 넘었다면 // 탈출을 위한 조건
return 검정색
만약 ray가 물체와 부딪혔다면
{
new_ray = 난반사 ray를 만든다.
return ray_color(new_ray, 오브젝트들을 가지고 있는 구조체 world, 최대반사횟수 - 1); // 재귀함수!
}
y벡터를 기준으로 그라데이션을 만든다(하늘 색상)
return 하늘색
}
C++
복사
이제 이러한 구조를 기억해두고 아래 부분을 공부해보자!
2) 난반사 표현하기!
그렇다면 우리는 이것을 어떻게 표현할 수 있을까?
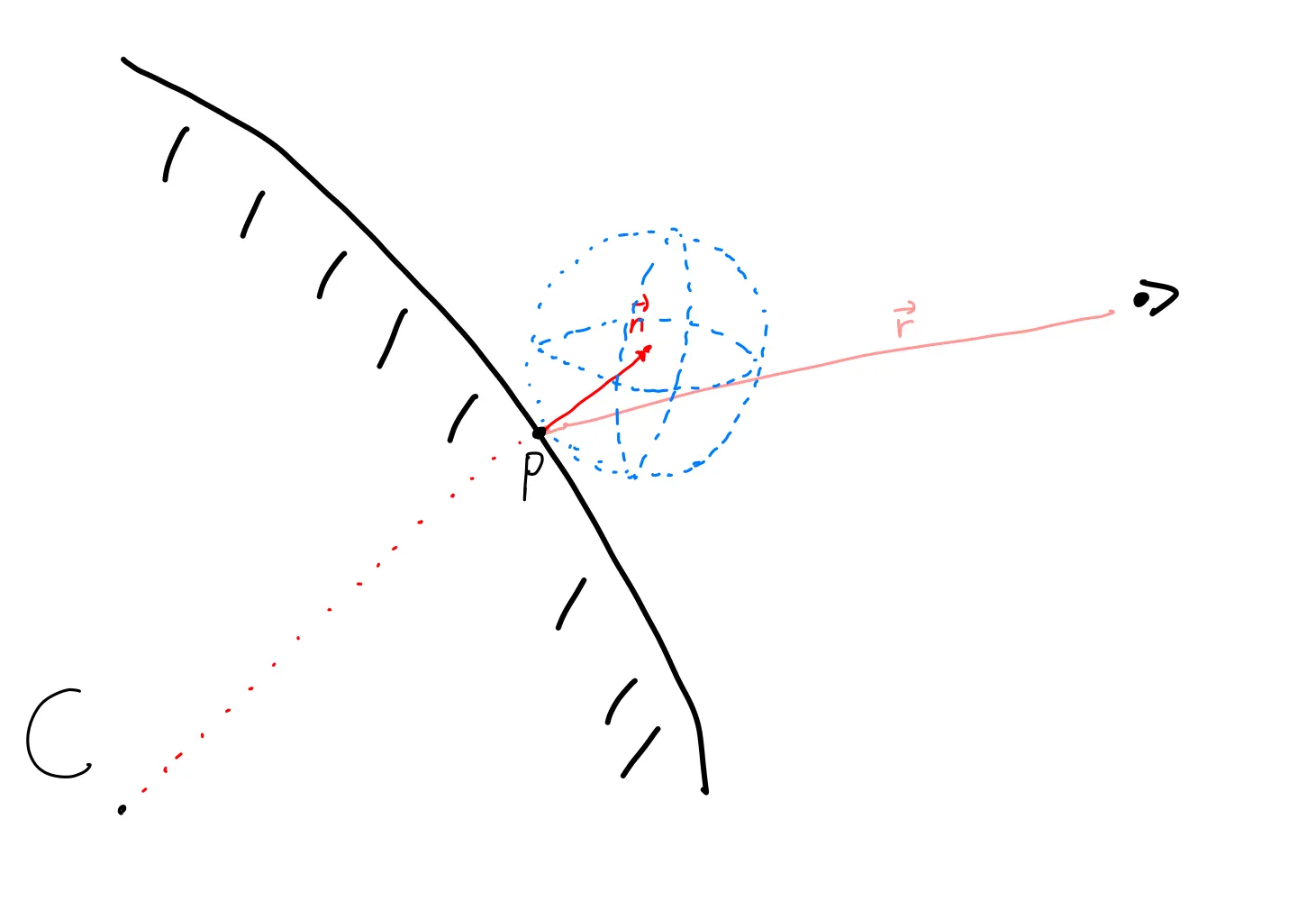
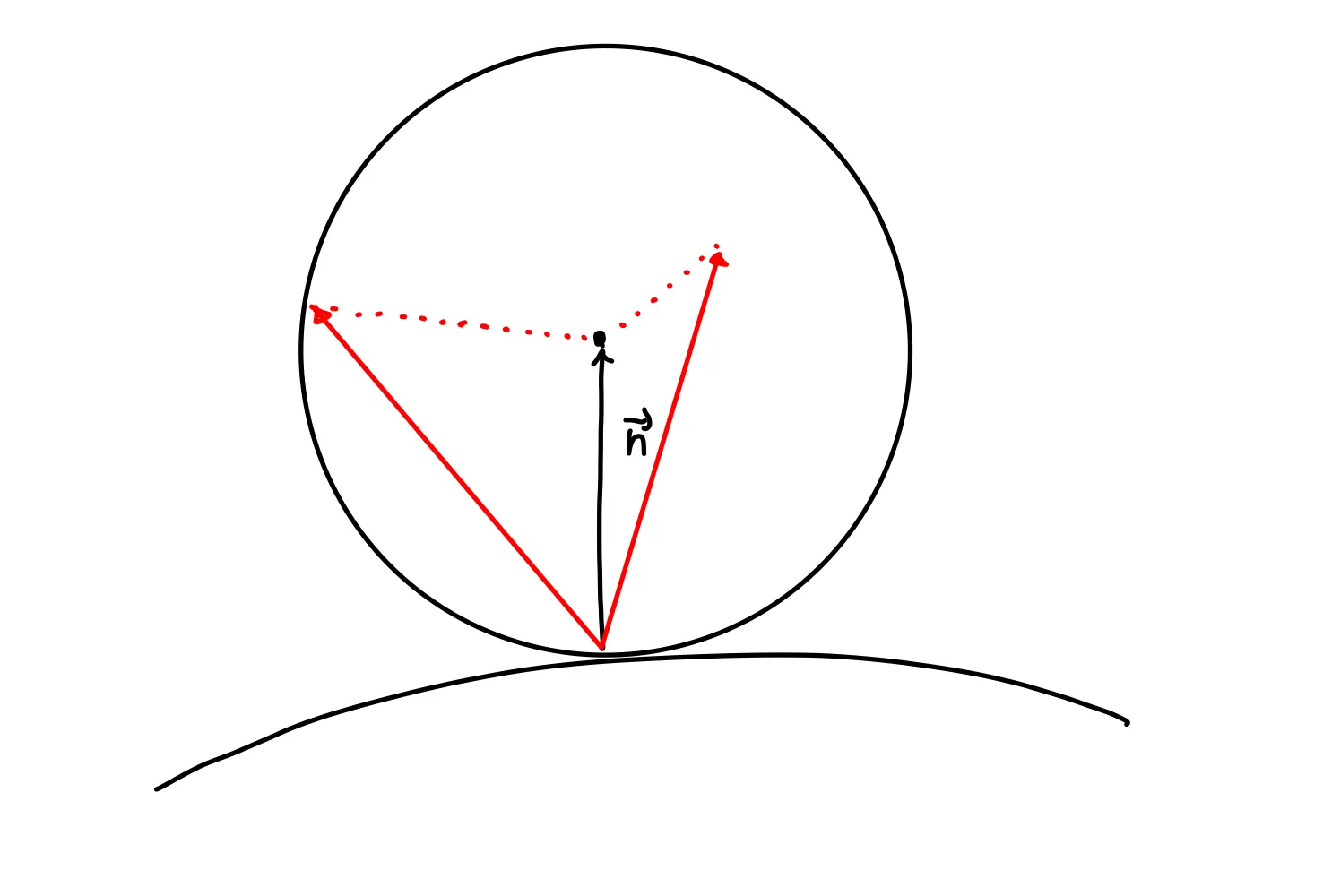
우리는 표면에서 난반사 되는 것을 표현하고 싶다! 우선 점 P에서의 법선 벡터 머리를 중앙으로 하고 반지름이 1인 구를 표면에 위치시킨다! 아래 사진을 보자!
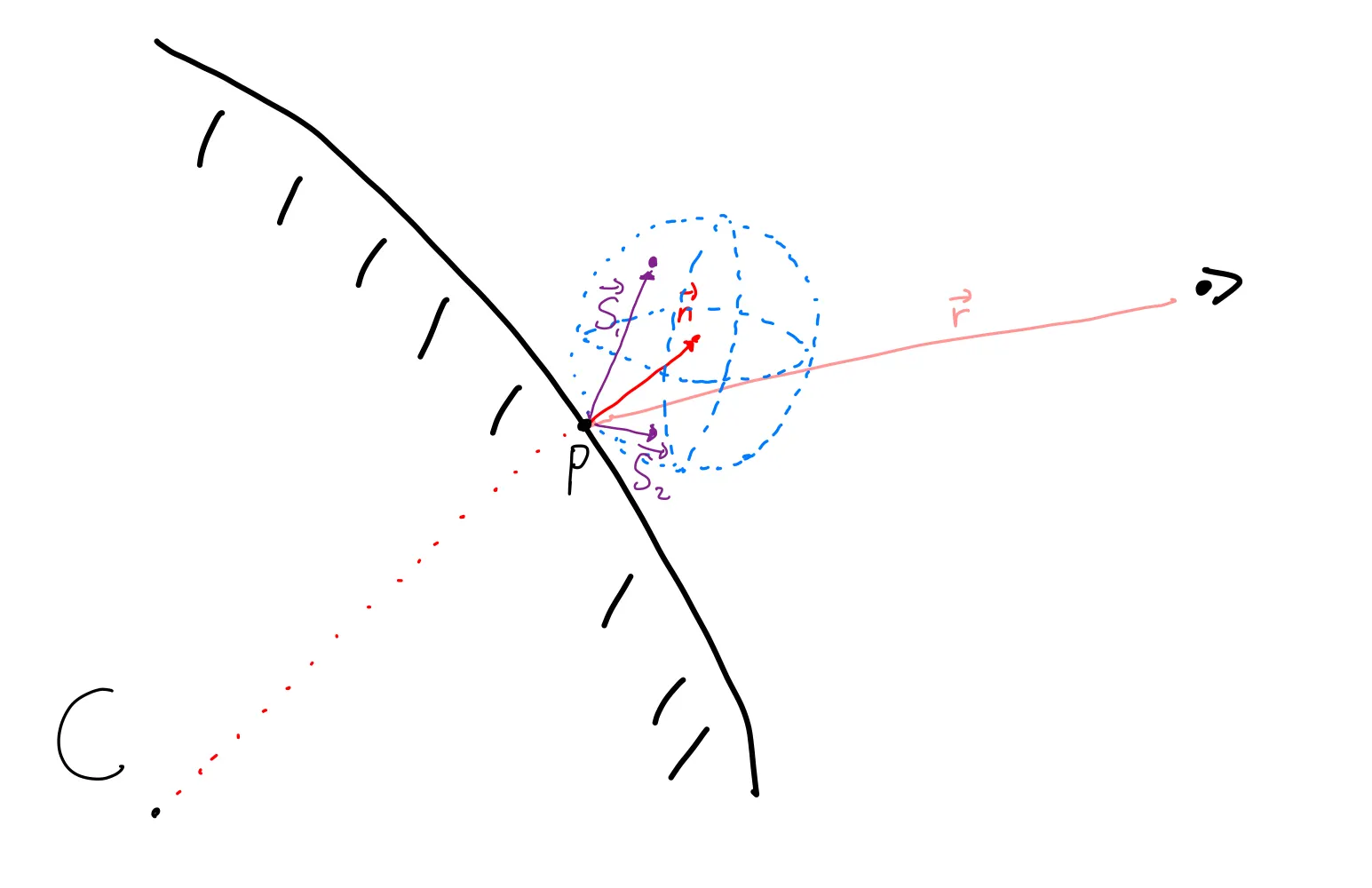
우리는 점 P에서 파란색 구 내부의 무작위 지점을 향한 ray를 만들면 마치 우리가 쏜 ray가 표면에 부딪혀서 난반사가 되는것 처럼 구현할 수 있는 것이다!! 아래의 보라색 벡터 S1, S2는 점P에서 구 위의 무작위 지점을 향한 벡터들이다.
그렇다면 이 구 내부의 지점을 어떻게 알 수 있을까? 교재에서는 아래와 같은 방법을 사용한다!
법선벡터의 머리 좌표 N(x, y, z)에서 각 성분에 -1 ~ 1 사이의 값을 랜덤으로 더해준다!
즉, random 함수를 활용해서 정말 무작위 ray를 만드는 것이다. 아래는 교재에서 사용하는 random함수들과 그것을 C로 변경해본 것이다.
// C++ code
class vec3 {
public:
...
inline static vec3 random() {
return vec3(random_double(), random_double(), random_double());
}
inline static vec3 random(double min, double max) {
return vec3(random_double(min,max), random_double(min,max), random_double(min,max));
}
// C code
t_vec random()
{
return vec(random_double(), random_double(), random_double());
}
t_vec random_minmax(double min, double max)
{
return vec(random_double_minmax(double min, double max),
random_double_minmax(double min, double max),
random_double_minmax(double min, double max));
}
C++
복사
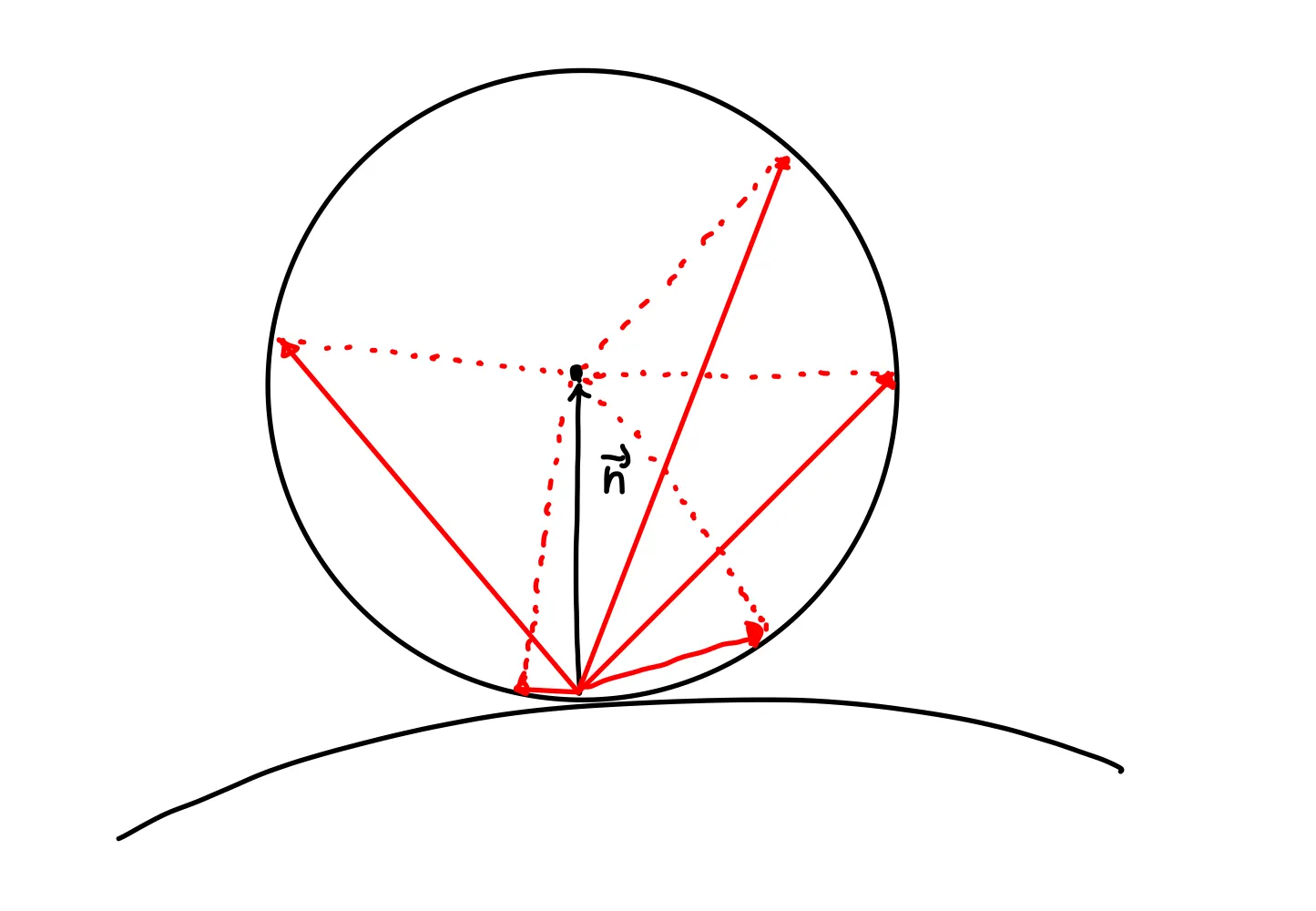
하지만 각 성분에 -1 ~ 1 사이의 값을 랜덤으로 더하면 구가 아니라 정육면체의 범위에 들어가게 된다. 그림이 조금 어지럽지만 대충 모든 성분에 1의 크기를 랜덤으로 더하거나 빼면 아래와 같은 결과가 나올 수 있다!
그래서 우리는 우리가 랜덤만든 벡터의 크기가 1을 넘으면 해당 벡터는 사용하지 않는 방식으로 진행할 것이다. 아래의 코드를 보자! 예를들어, vec(1, 1, -1) 과 같은 벡터는 크기가 이기 때문에 불가능한 것이다!
// C++ code
vec3 random_in_unit_sphere() {
while (true) {
auto p = vec3::random(-1,1);
if (p.length_squared() >= 1) continue;
return p;
}
}
// C code
t_vec random_in_unit_sphere()
{
t_vec p;
while (1) {
p = vec(random_minmax(-1,1), random_minmax(-1,1), random_minmax(-1,1));
if (p.length_squared() >= 1)
continue;
return (p);
}
}
C++
복사
이제 이전의 코드에서 바뀐부분만 살펴보면 뒷부분에 random_in_unit_sphere() 함수를 통해 무작위 반사 벡터를 구하는 것을 볼 수 있다!
// C++ Code
if (world.hit(r, 0, infinity, rec)) {
point3 target = rec.p + rec.normal + random_in_unit_sphere();
return 0.5 * ray_color(ray(rec.p, target - rec.p), world);
}
// C code
if (world.hit(r, 0, infinity, rec))
{
// 벡터 3개를 더해주는 함수가 필요하다. 아니면 두개를 더하는 함수를 두번 사용해도 OK!
t_vec target = vec_add3(rec.p, rec.normal, random_in_unit_sphere());
return 0.5 * ray_color(ray(rec.p, target - rec.p), world);
}
C++
복사
여기서 의문점이 생긴다. 이 코드에서 마지막에 0.5 * ray_color(ray(rec.p, target - rec.p), world); 부분이 이상하다고 느꼈을 것이다! 엥!? 대체 왜 0.5를 곱해주는 것일까?
그 이유는 위에서 말했던 흡수와 관련된 내용이다. 빛이 구에 부딪히면 모든 빛을 반사하는 것이 아니라 일부분은 흡수하기 때문에 반사돼서 나오는 ray의 색깔을 반사될 때마다 절반을 나눠서 점점 빛이 흡수되어 어두워지게 만드는 것이다!
여기에 추가로 빛이 최대 반사될 수 있는 횟수를 설정해서 설정한 횟수를 넘어간다면 대부분의 빛이 이미 흡수되었을 것이기때문에 검정색을 return하고 반사를 중단하는 것이다!
// C++ code
color ray_color(const ray& r, const hittable& world, int depth) {
hit_record rec;
if (depth <= 0)
return color(0,0,0); // 설정한 횟수를 넘어간다면 검정색!
if (world.hit(r, 0, infinity, rec)) {
point3 target = rec.p + rec.normal + random_in_unit_sphere();
return 0.5 * ray_color(ray(rec.p, target - rec.p), world, depth-1);
}
vec3 unit_direction = unit_vector(r.direction());
auto t = 0.5*(unit_direction.y() + 1.0);
return (1.0-t)*color(1.0, 1.0, 1.0) + t*color(0.5, 0.7, 1.0);
}
C++
복사
main()에서 max_depth를 50정도로 설정해주면 아래와 같은 화면이 나오게 된다!
3) Using Gamma Correction for Accurate Color Intensity
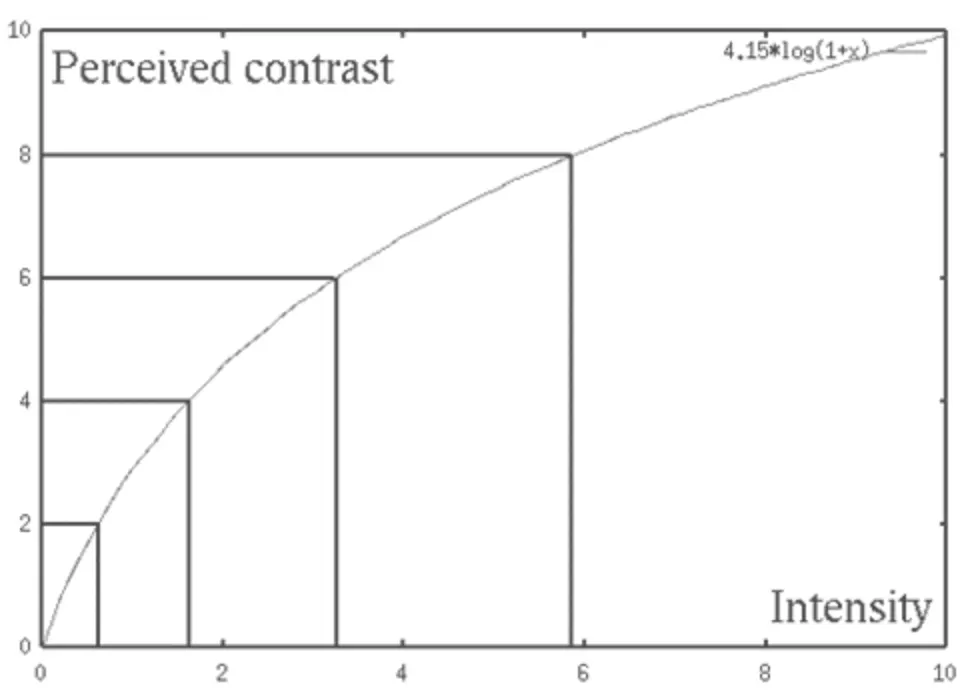
감마 보정을 활용해서 조금 더 정확한 색상을 표현해보자! 감마 보정이란, 사람의 눈이 밝기에 비선형적으로 대응하기 때문에 실제 출력하는 화면의 색을 실제 사람이 부드럽게 인지할 수 있도록 조정해 주는 것이다.
즉, 밝기가 어두울 때 사람의 눈은 밝기의 변화에 민감하게 반응하고, 밝기가 밝을 때 사람의 눈은 밝기의 변화에 둔감하게 반응한다! 따라서 한정적인 표현 영역(bit)으로 분배를 해야 한다면 밝은 쪽 보다는 어두운 쪽에 그 비중을 크게 두는 것이 좋다.
그래서 우리는 비선형 전달 함수가 필요한 것이다!
기본적으로 2.2라는 감마값을 기준으로 지수관계를 계산하지만 본문에서는 근사치인 를 활용한다.
auto scale = 1.0 / samples_per_pixel;
r = sqrt(scale * r);
g = sqrt(scale * g);
b = sqrt(scale * b);
C++
복사
마지막 부분에 clamp()를 해주는 이유는 antialiasing과정을 거치면서 r의 값이 1을 넘어가는 경우가 발생할 수 있다. clamp함수는 이때를 대비해서 최대값과 최소값을 고정시켜주는 역할을 한다.
out << static_cast<int>(256 * clamp(r, 0.0, 0.999)) << ' '
<< static_cast<int>(256 * clamp(g, 0.0, 0.999)) << ' '
<< static_cast<int>(256 * clamp(b, 0.0, 0.999)) << '\n';
C++
복사
이제 이 과정을 거치면 조금더 밝게 처리된 구를 확인할 수 있다!
4) Fixing Shadow Acne
이 과정에서 우리는 t_min값을 0으로 두고 위 과정을 진행해 왔다. 하지만 0에 가까운 근사치(0.001 혹은 0.00000001) 도 우리는 무시해주어야 한다. 왜냐하면 반사된 광선 중 일부는 정확하게 t = 0을 만족하지 않을 수 있기 때문이다!
if (world.hit(r, 0.001, infinity, rec))
C++
복사
5) True Lambertian Reflection
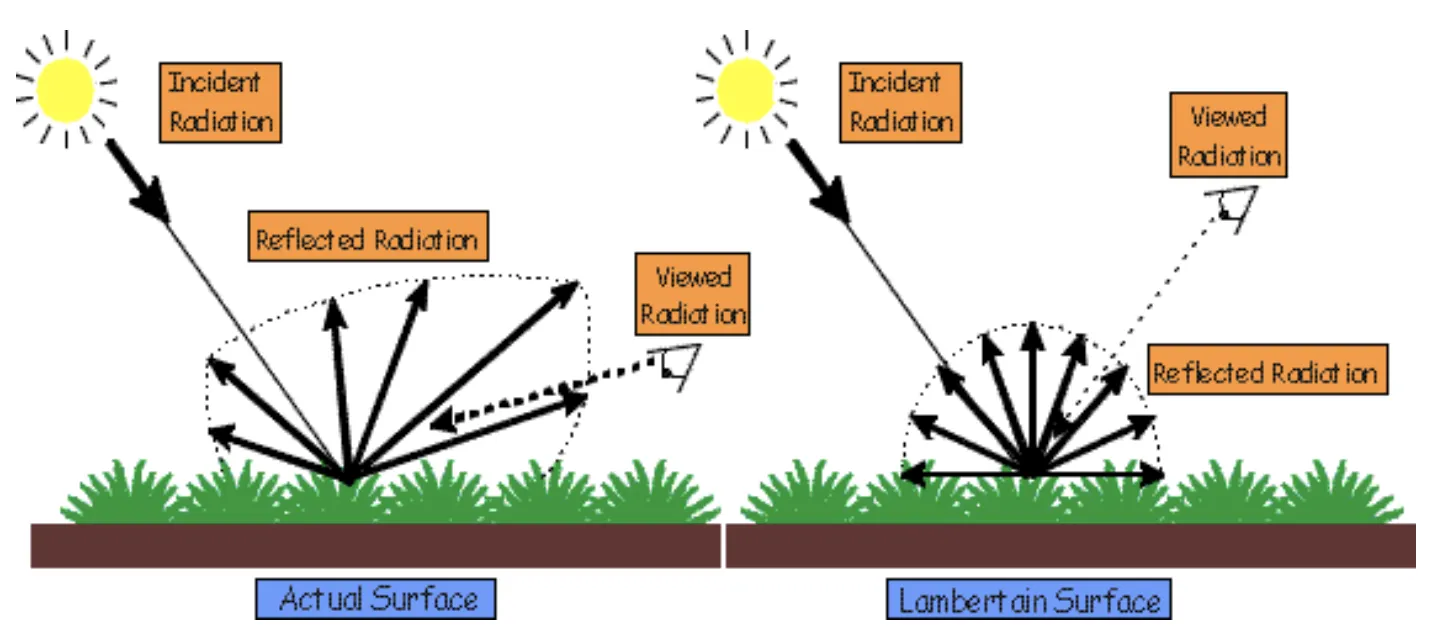
램버시안 반사 혹은 램버시안이라고 불리는 것은 그래픽스나 복사이론에서 엄청나게 중요한 개념 중 하나이다!! 간단하게 말하면 Lambertian surface는 모든 방향에서 보아도 똑같은 밝기로 보이는 표면을 뜻한다. Lambertian reflection는 이러한 표면에서 일어나는 반사를 의미한다.
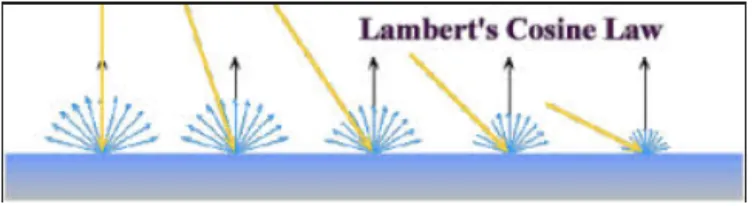
여기서 Lambert's Cosine Law(램버트 코사인 법칙)이라는 중요한 법칙이 나온다!
Lambert's Cosine Law(램버트 코사인 법칙)
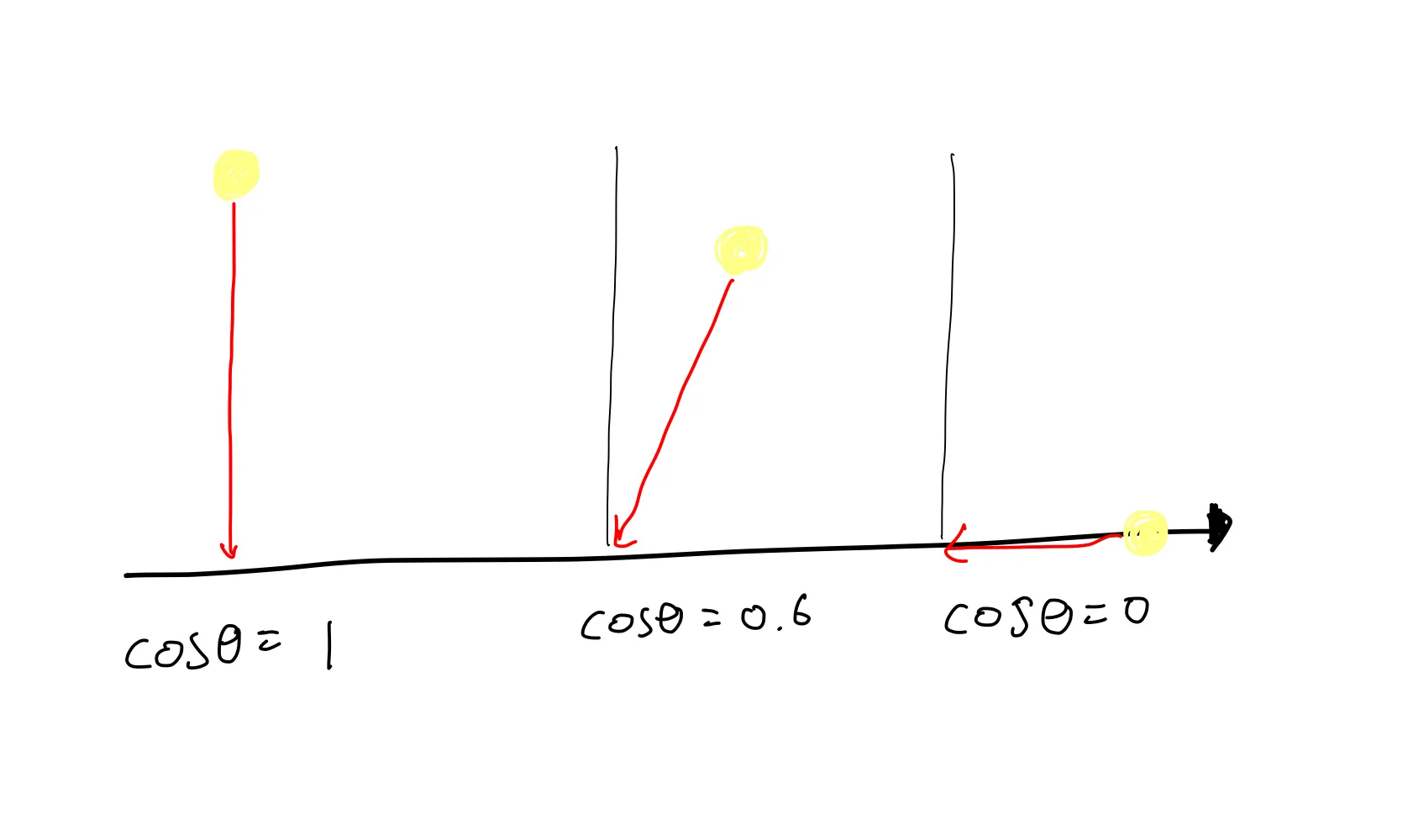
Lambertian surface를 바라볼 때의 광도는 표면의 법선벡터와 시선벡터 사이각의 코사인에 비례한다.
즉, 법선과 일치하는 면에서 봤을때가 비스듬히 봤을때보다 더 많은 광도를 가진다는 의미이다.
이와 같은 성질을 가지는 표면을 바로 Lambertian이라고 하며 이러한 표면을 가지는 물체는 어떤 방향에서 보던지 같은 면이여야 한다.
우리가 위에서 만든 난반사 공식을 활용하면 완전한 Lanbertian Surface를 표현하는 방식이 아니다. 우리는 이 식을 수정하여 모든 방향으로 일정하게 반사되는 표면을 구현해 볼 것이다. 즉 아래 과정을 통해 Lambertian Surface를 가지는 도형을 만들어 보는 것이다!
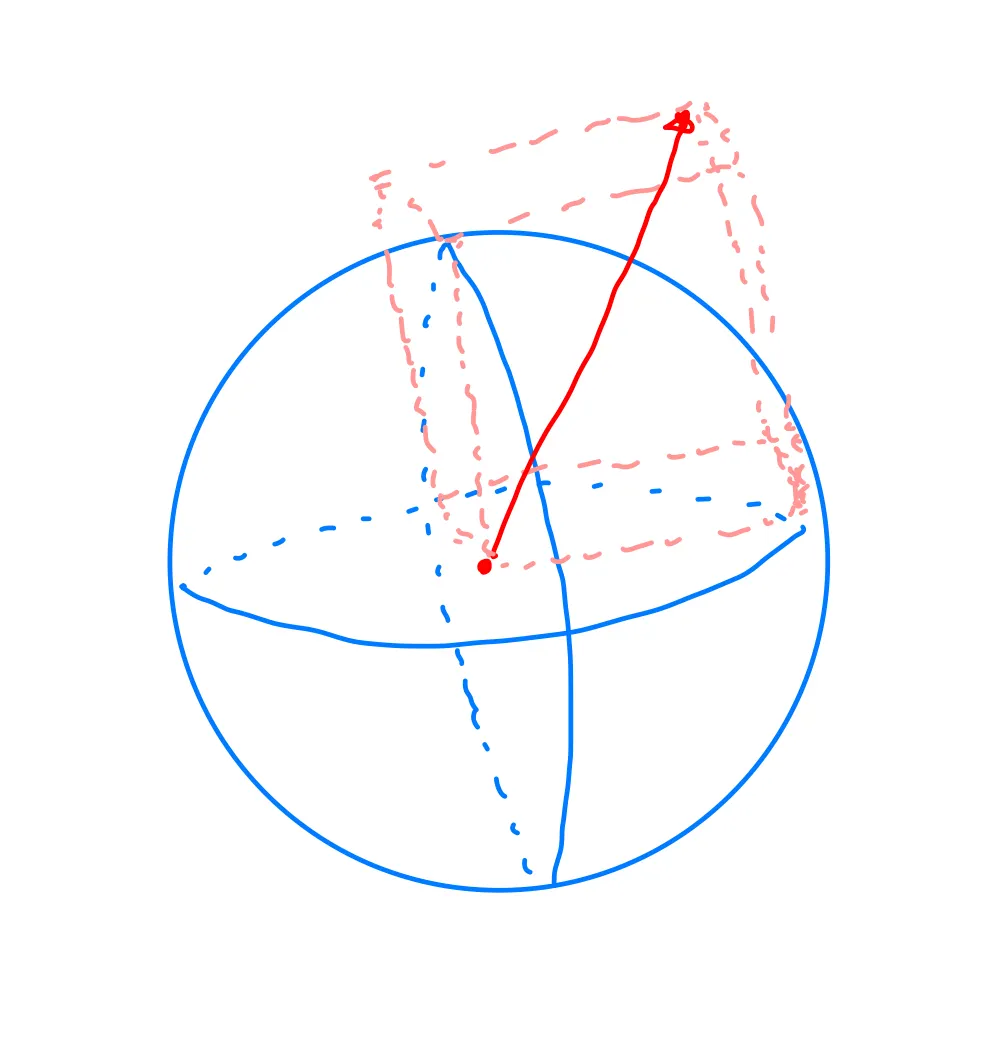
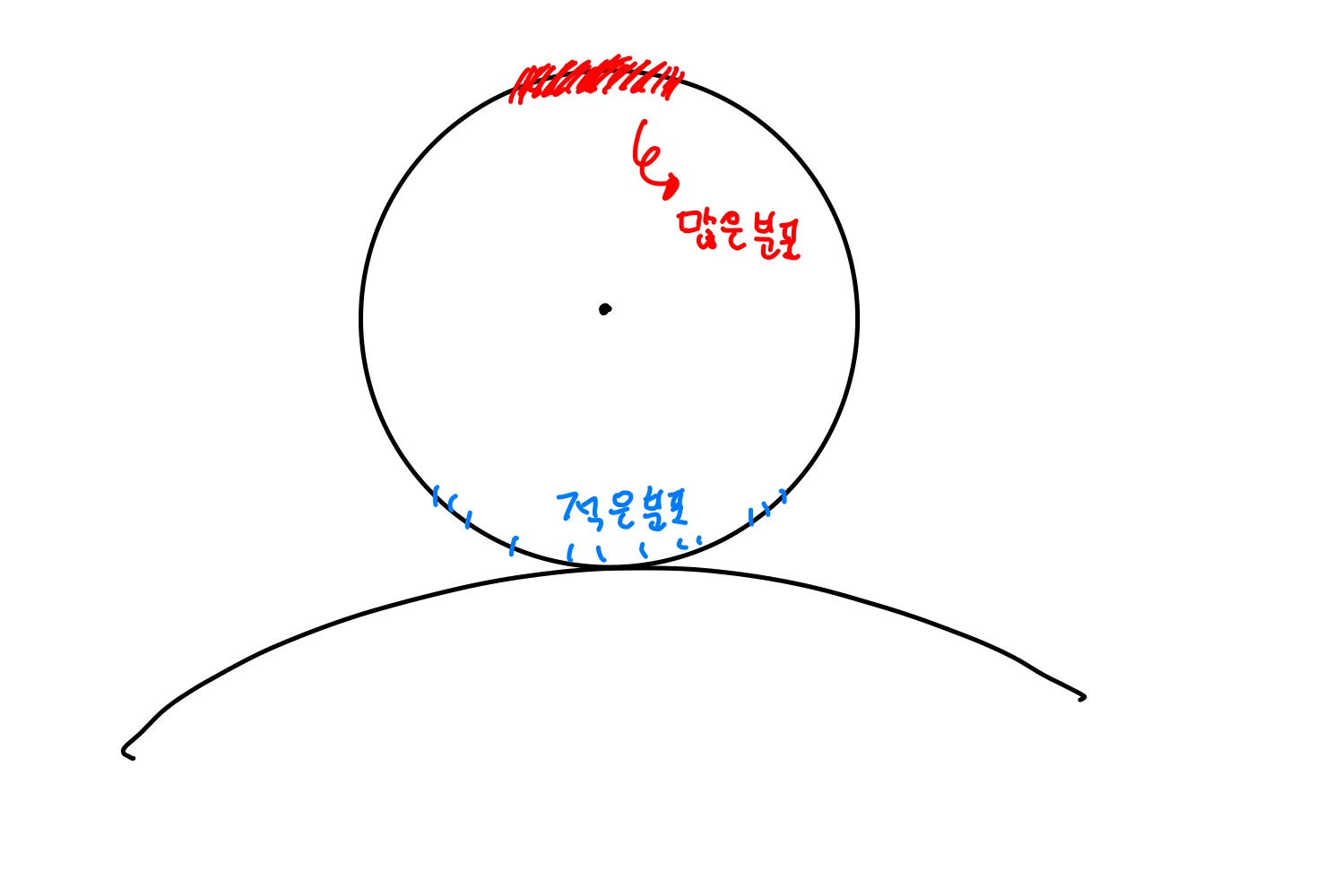
우선 Lambertian surface를 적용하기전에 위에서 만든 공식의 문제점을 살펴보자! Lambertian suface는 cos에 비례하는 법칙인데 위에서 만든 공식은 cos에 비례하지 않고 cos^3에 비례한다. 아래 사진을 보자
기존의 방식으로 계산하면 랜덤벡터의 크기에 따라 구의 상단에만 많은 분포를 가지는 벡터를 만들게 된다.
이러한 문제점을 해결하기위해 우리는 랜덤벡터를 단위벡터로 만들어서 크기를 1로 고정시킨 뒤 생성되는 모든 벡터가 구 표면상의 점에 머리를 위치하도록 만들어준다. 바로 아래 그림처럼 말이다!
이렇게되면 조금더 정확하고 균등한 cos분포를 가지는 벡터를 만들 수 있는 것이다!!
// 기존의 랜덤벡터를 단위벡터로 만들어준다.
vec3 random_unit_vector() {
return unit_vector(random_in_unit_sphere());
}
C++
복사
// 계산 부분을 단위벡터로 바꾸어준다.
// C++ code
point3 target = rec.p + rec.normal + random_unit_vector();
// C code
t_vec target = vec_add3(rec.p, rec.normal, random_unit_vector());
C++
복사
6) An Alternative Diffuse Formulation
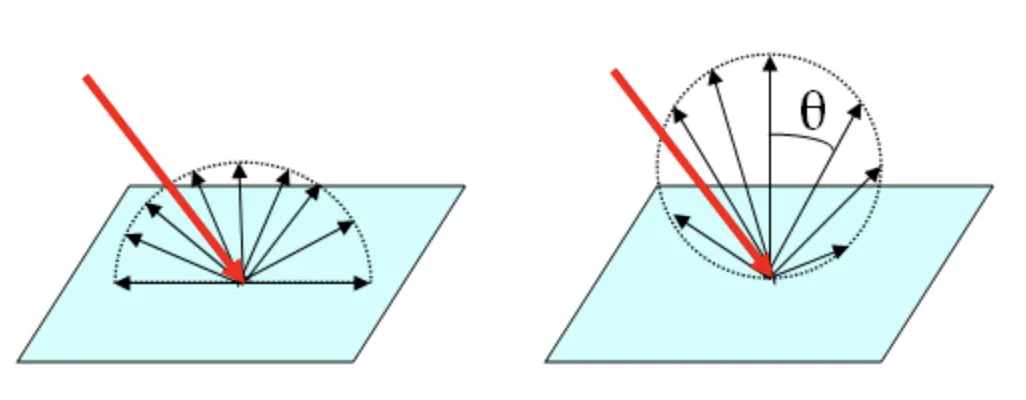
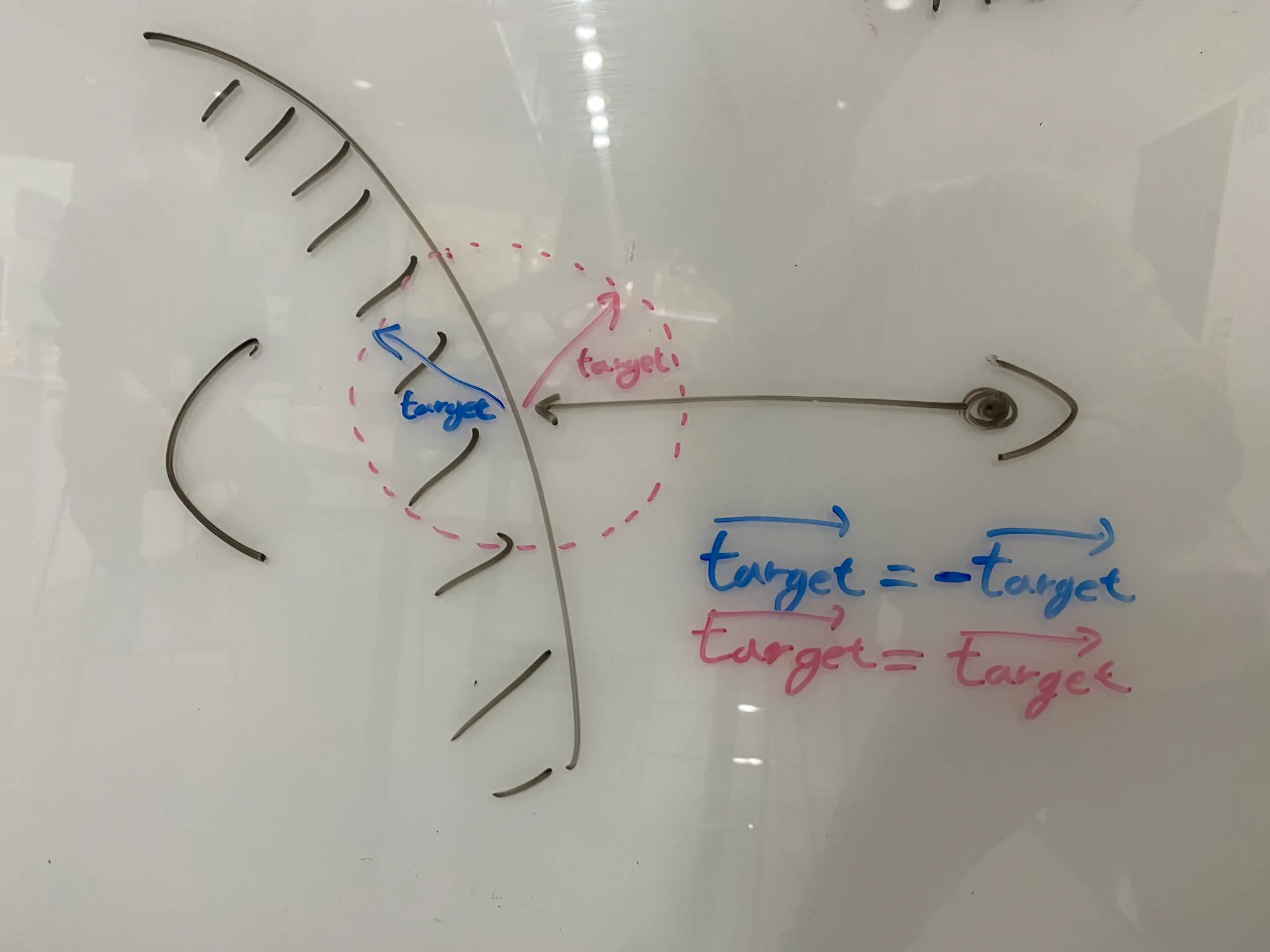
우리가 위에서 만든 난반사 ray는 오른쪽과 같은 형태이다. 하지만 Lambertian reflection을 제대로 구현하려면 왼쪽과 같은 형태로 나타나야 한다.
그래서 우리는 식을 조금 바꾸기로 했다! 점 P와 P에서의 법선벡터 normal을 더해주는 벡터에서 법선벡터를 빼고 계산을 하면 된다!
// C++ code
point3 target = rec.p + random_unit_vector();
C++
복사
이렇게 하면 점P에서 뻗어나가는 모든 벡터의 크기가 같아지면서 완전확산면(램퍼시안 표면)을 만족한다.
하지만 이 경우에 고려해야할 문제가 생긴다! 바로 구 내부로 들어가는 벡터에 대한 부분이다. 아래 그림을 보자.
우리는 점P 에서 랜덤하게 반사되는 target벡터를 구해야하는데 그 벡터가 부딪히는 구 내부를 향하게 된다면 반사의 의미가 없게 되는 것이다. 이때 우리는 또 내적을 활용해서 이 문제를 쉽게 해결할 수 있다. 이전에 내적을 활용하는 것을 배웠기 때문에 쉽게 이해할 수 있을 것이다!
// C++ code
vec3 random_in_hemisphere(const vec3& normal) {
vec3 in_unit_sphere = random_in_unit_sphere();
// P에서의 법선벡터와 반사벡터의 내적, 즉, cos값이 양수라면? 그대로, 음수라면? 방향을 반대로
if (dot(in_unit_sphere, normal) > 0.0)
return in_unit_sphere;
else
return -in_unit_sphere;
}
C++
복사
이제 우리는 이 함수를 활용해서 랜덤벡터를 만들 수 있게 된다!
// C++ code
point3 target = rec.p + random_in_hemisphere(rec.normal);
// C code
t_vec target = vec_add(rec.p, random_in_hemisphere(rec.normal));
C++
복사
Make!
드디어 8장에서 원하는 결과물을 얻어냈다!!
만약 오류가 난다면 교재를 보면서 단위벡터, 법선벡터의 방향과 상수값에서 차이가 있는지 확인해보자!